# algorithm
**Repository Path**: YYgyf/algorithm
## Basic Information
- **Project Name**: algorithm
- **Description**: No description available
- **Primary Language**: Java
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 0
- **Created**: 2018-10-11
- **Last Updated**: 2021-04-15
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
### **时间复杂度和空间复杂度**
#### **为什么需要复杂度分析**
我们把代码跑一边通过监控、统计就可以得到算法所执行的时间和占用的内存的大小为什么还要做时间、空间复杂度分析?因为这种统计算法有很大的局限性,也叫做 事后统计法
-
硬件的影响(测试结果依赖于测试环境)
-
例如:在不同的处理器上测试,结果千差万别
-
测试结果受数据规模的影响
-
例如:同一种算法在不同的待排序的数据中,执行时间会有很大的差别
#### **大O表示法**
算法的执行效率,简单来说,就是算法的执行时间,例如:求的和 1,2,3,4...n
```java
1 public int sum(int n) {
2 int sum;
3 for (int i = 1; i < = n; i++) {
4 sum += i;
5 }
6 return sum;
7 }
```
Java代码执行依靠于JVM的指令,上面的每行代码转化为JVM指令执行的时候执行的时间也是不一样,所以要要假设每行代码执行的时间都一样,为unit_time,在这个假设基础来计算这段代码执行的时间。第二行需要2个unit_time,3,4行运行了n次,都需要n个unit_time,所以总的就是(2n+1)*unit_time。所以可以看出所有代码执行的总时间T(n)和每行代码执行的次数成正比。把这个规律总结成一个公式
就是:大O登场
T(n)=Of(n)
T(n):表示代码执行的时间
f(n):表示每行代码执行次数的总和
O; 表示代码执行的时间T(n)与f(n)成正比的关系
n: 表示数据规模
所以求和例子中:T(n)=O(2n+1);这就是大O时间复杂度表示,大O表示的不是真正代码执行的时间,它表示的是代码执行的时间与随数据规模(n)增长的变化趋势。所以叫做"渐进时间复杂度“,简称"时间复杂度"。当n很大的时候,公式中的低阶、常数、系数并不能左右增长趋势,所以可以忽略。
只用记下最大量级就可以了,所以上面的求和代码的时间复杂度是 T(n)=O(n).
#### **时间复杂度分析**
1.只关注循环执行次数最多的代码
大O这种复杂度只表示一种变化趋势,通常会忽略掉低阶、系数阶、常数阶。只关注最大量阶就可以了
```java
1 public int sum(int n) {
2 int sum;
3 for (int i = 1; i < = n; i++) {
4 sum += i;
5 }
6 return sum;
7 }
```
第一二执行的是常数级别,与n无关对复杂度没有影响。循环最多的是第三四行,这两行代码被执行n次,所以时间复杂度是n
2.乘法法则嵌套代码的复杂度等于嵌套内外代码复杂度的成绩
也就是说T1(n)=O(n) T2(n)=O(n2),那么T1*T2=O(n3);
#### **常见的时间复杂度**
1.O(1)
O(1)只是常量级时间复杂度的一种表示,并不是只执行了一行代码,比如这行代码它的时间复杂度是O{1},而不是O(3)
```java
int a = 1;
int b = 2;
int sun = b - a;
```
2.O(n)
```java
for (int i = 0; i < n; i++) {
}
```
3.o(n2)
```java
for (int i = 0; i < n; i++) {
for (int j = 0; j
2^x=n,转换x=log2ⁿ,所以这行代码的执行时间是O(log2ⁿ),如果代码这样的
```java
1 int i = 1;
2 while (i < =n) {
3 i = i * 3;
4 }
```
可以看出这段代码的时间复杂度是O(log3ⁿ),因为log3ⁿ=log3²*log2ⁿ,log3²是一个常数,所以这段代码的时间复杂度还是O(log2ⁿ),把所有的对数阶的时间复杂度统称为O(longn)。
O(nlogn)等于O(n)*O(logn)就是把上面代码循环的n次,
```java
for (int j = 0; j
#### **空间复杂度分析**
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系,空间复杂度也叫作渐进空间复杂度,表示算法的存储空间与数据规模之间的关系。时间复杂度和空间复杂度分析是一样的,常见的空间复杂度O(1)、O(n)、O(n²),像O(logn)、O(nlogn),平时很少用到。例如:
```java
int i, j, temp;
for(i=0; i最好情况时间复杂度 、最坏时间复杂度、平均时间复杂度
2.平均情况时间复杂度
要查找的x变量在数组中的位置有n+!中情况,可以把每种情况下要查找遍历的元素个数累加起来然后/n+1,就可以得到遍历元素个数的平均值
 简化之后得到的时间复杂度就是o(n),但是n+1种情况出现的概率并不是一样的,假设在数组中和不在数组中的概率都为1/2,要查找的数据出现在0-n-1这n个位置的概率也一样,为1/n,所以要查找的数据出现在0-n-1中的任意位置的概率就是/(2n)。
简化之后得到的时间复杂度就是o(n),但是n+1种情况出现的概率并不是一样的,假设在数组中和不在数组中的概率都为1/2,要查找的数据出现在0-n-1这n个位置的概率也一样,为1/n,所以要查找的数据出现在0-n-1中的任意位置的概率就是/(2n)。
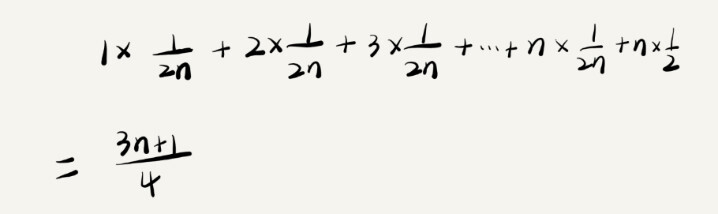 这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度,代码的加权平均值为(3n+1)/4,用大O表示仍然是O(n)。
只有同一块代码在不同的情况下,时间复杂度有量级的差距,才会使用这三种复杂度表示法来区分。
这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度,代码的加权平均值为(3n+1)/4,用大O表示仍然是O(n)。
只有同一块代码在不同的情况下,时间复杂度有量级的差距,才会使用这三种复杂度表示法来区分。
 简化之后得到的时间复杂度就是o(n),但是n+1种情况出现的概率并不是一样的,假设在数组中和不在数组中的概率都为1/2,要查找的数据出现在0-n-1这n个位置的概率也一样,为1/n,所以要查找的数据出现在0-n-1中的任意位置的概率就是/(2n)。
简化之后得到的时间复杂度就是o(n),但是n+1种情况出现的概率并不是一样的,假设在数组中和不在数组中的概率都为1/2,要查找的数据出现在0-n-1这n个位置的概率也一样,为1/n,所以要查找的数据出现在0-n-1中的任意位置的概率就是/(2n)。
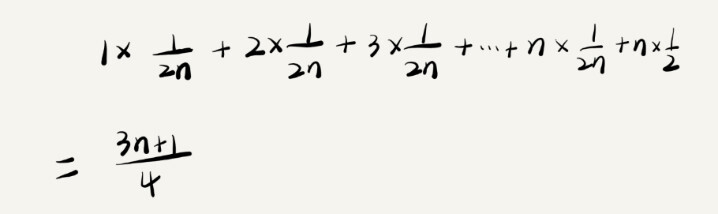 这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度,代码的加权平均值为(3n+1)/4,用大O表示仍然是O(n)。
只有同一块代码在不同的情况下,时间复杂度有量级的差距,才会使用这三种复杂度表示法来区分。
这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度,代码的加权平均值为(3n+1)/4,用大O表示仍然是O(n)。
只有同一块代码在不同的情况下,时间复杂度有量级的差距,才会使用这三种复杂度表示法来区分。