# db-demo
**Repository Path**: devmazhao/db-demo
## Basic Information
- **Project Name**: db-demo
- **Description**: 动态数据源测试和学习动态数据源测试和学习动态数据源测试和学习
- **Primary Language**: Unknown
- **License**: MulanPSL-2.0
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 0
- **Created**: 2022-06-29
- **Last Updated**: 2024-07-11
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# [2322. 从树中删除边的最小分数](https://leetcode.cn/problems/minimum-score-after-removals-on-a-tree)
[English Version](/solution/2300-2399/2322.Minimum%20Score%20After%20Removals%20on%20a%20Tree/README_EN.md)
## 题目描述
存在一棵无向连通树,树中有编号从 0 到 n - 1 的 n 个节点, 以及 n - 1 条边。
给你一个下标从 0 开始的整数数组 nums ,长度为 n ,其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。
删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案,定义如下步骤以计算其分数:
- 分别获取三个组件 每个 组件中所有节点值的异或值。
- 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
- 例如,三个组件的节点值分别是:
[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ,最小异或值是 3 ,分数是 8 - 3 = 5 。
返回在给定树上执行任意删除边方案可能的 最小 分数。
示例 1:
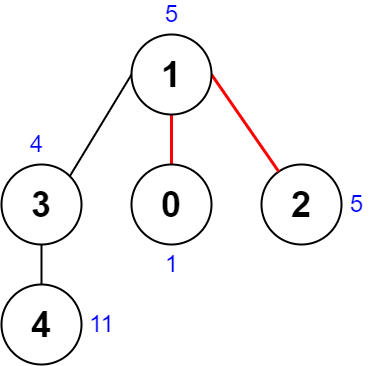
输入:nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:9
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ,值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ,值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ,值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值,10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。
示例 2:
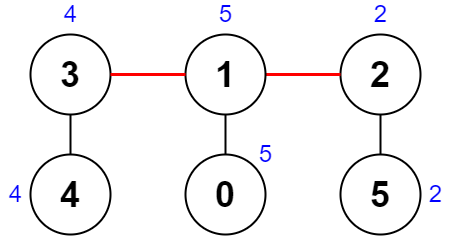
输入:nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出:0
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ,值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ,值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ,值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值,0 - 0 = 0 。
无法获得比 0 更小的分数 0 。
提示:
n == nums.length3 <= n <= 10001 <= nums[i] <= 108edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges 表示一棵有效的树
## 解法
**方法一:DFS + 子树异或和**
枚举 $[0, n)$ 的每个点 $i$ 作为树的根节点,将根节点与某个子节点相连的边作为第一条被删除的边。这样我们就获得了两个连通块,我们记包含根节点 $i$ 的连通块为 $A$,不包含根节点 $i$ 的连通块为 $B$。
在 $A$ 中枚举第二条被删除的边。那么 $A$ 也会被划分成两个连通块 $C$ 和 $D$。
记每个连通块的异或和为 $S_i$,那么对于枚举的每一种情况,得到的分数为 $max(S_B, S_C, S_D)-min(S_B, S_C, S_D))$。求所有情况的最小值作为答案。
### **Python3**
```python
class Solution:
def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
def dfs(i, fa, x):
res = nums[i]
for j in g[i]:
if j != fa and j != x:
res ^= dfs(j, i, x)
return res
def dfs2(i, fa, x):
nonlocal s, s1, ans
res = nums[i]
for j in g[i]:
if j != fa and j != x:
a = dfs2(j, i, x)
res ^= a
b = s1 ^ a
c = s ^ s1
t = max(a, b, c) - min(a, b, c)
ans = min(ans, t)
return res
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
s = 0
for v in nums:
s ^= v
n = len(nums)
ans = inf
for i in range(n):
for j in g[i]:
s1 = dfs(i, -1, j)
dfs2(i, -1, j)
return ans
```
### **Java**
```java
class Solution {
private int s;
private int s1;
private int n;
private int ans = Integer.MAX_VALUE;
private int[] nums;
private List[] g;
public int minimumScore(int[] nums, int[][] edges) {
n = nums.length;
g = new List[n];
this.nums = nums;
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<>();
}
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
for (int v : nums) {
s ^= v;
}
for (int i = 0; i < n; ++i) {
for (int j : g[i]) {
s1 = dfs(i, -1, j);
dfs2(i, -1, j);
}
}
return ans;
}
private int dfs(int i, int fa, int x) {
int res = nums[i];
for (int j : g[i]) {
if (j != fa && j != x) {
res ^= dfs(j, i, x);
}
}
return res;
}
private int dfs2(int i, int fa, int x) {
int res = nums[i];
for (int j : g[i]) {
if (j != fa && j != x) {
int a = dfs2(j, i, x);
res ^= a;
int b = s1 ^ a;
int c = s ^ s1;
int t = Math.max(Math.max(a, b), c) - Math.min(Math.min(a, b), c);
ans = Math.min(ans, t);
}
}
return res;
}
}
```
### **C++**
```cpp
class Solution {
public:
vector nums;
int s;
int s1;
int n;
int ans = INT_MAX;
vector> g;
int minimumScore(vector& nums, vector>& edges) {
n = nums.size();
g.resize(n, vector());
for (auto& e : edges)
{
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
for (int& v : nums) s ^= v;
this->nums = nums;
for (int i = 0; i < n; ++i)
{
for (int j : g[i])
{
s1 = dfs(i, -1, j);
dfs2(i, -1, j);
}
}
return ans;
}
int dfs(int i, int fa, int x) {
int res = nums[i];
for (int j : g[i]) if (j != fa && j != x) res ^= dfs(j, i, x);
return res;
}
int dfs2(int i, int fa, int x) {
int res = nums[i];
for (int j : g[i]) if (j != fa && j != x)
{
int a = dfs2(j, i, x);
res ^= a;
int b = s1 ^ a;
int c = s ^ s1;
int t = max(max(a, b), c) - min(min(a, b), c);
ans = min(ans, t);
}
return res;
}
};
```
### **Go**
```go
func minimumScore(nums []int, edges [][]int) int {
n := len(nums)
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
s := 0
for _, v := range nums {
s ^= v
}
s1 := 0
ans := math.MaxInt32
var dfs func(int, int, int) int
var dfs2 func(int, int, int) int
dfs = func(i, fa, x int) int {
res := nums[i]
for _, j := range g[i] {
if j != fa && j != x {
res ^= dfs(j, i, x)
}
}
return res
}
dfs2 = func(i, fa, x int) int {
res := nums[i]
for _, j := range g[i] {
if j != fa && j != x {
a := dfs2(j, i, x)
res ^= a
b := s1 ^ a
c := s ^ s1
t := max(max(a, b), c) - min(min(a, b), c)
ans = min(ans, t)
}
}
return res
}
for i := 0; i < n; i++ {
for _, j := range g[i] {
s1 = dfs(i, -1, j)
dfs2(i, -1, j)
}
}
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
```
### **TypeScript**
```ts
```
### **...**
```
```

