# RVM-MATLAB **Repository Path**: gshang/RVM-MATLAB ## Basic Information - **Project Name**: RVM-MATLAB - **Description**: No description available - **Primary Language**: Unknown - **License**: Not specified - **Default Branch**: master - **Homepage**: None - **GVP Project**: No ## Statistics - **Stars**: 0 - **Forks**: 0 - **Created**: 2022-02-06 - **Last Updated**: 2022-02-06 ## Categories & Tags **Categories**: Uncategorized **Tags**: None ## README

Relevance Vector Machine (RVM)

MATLAB code for Relevance Vector Machine

Version 2.1, 31-AUG-2021

Email: iqiukp@outlook.com

[![View Relevance Vector Machine (RVM) on File Exchange](https://www.mathworks.com/matlabcentral/images/matlab-file-exchange.svg)](https://www.mathworks.com/matlabcentral/fileexchange/69407-relevance-vector-machine-rvm)
## Main features - RVM model for binary classification (RVC) or regression (RVR) - Multiple kinds of kernel functions (linear, gaussian, polynomial, sigmoid, laplacian) - Hybrid kernel functions (K =w1×K1+w2×K2+...+wn×Kn) - Parameter Optimization using Bayesian optimization, Genetic Algorithm, and Particle Swarm Optimization ## Notices - This version of the code is not compatible with the versions lower than R2016b. - Detailed applications please see the demonstrations. - This code is for reference only. ## Citation ``` @article{tipping2001sparse, title={Sparse Bayesian learning and the relevance vector machine}, author={Tipping, Michael E}, journal={Journal of machine learning research}, volume={1}, number={Jun}, pages={211--244}, year={2001} } ``` ``` @article{qiu2021soft, title={Soft sensor development based on kernel dynamic time warping and a relevant vector machine for unequal-length batch processes}, author={Qiu, Kepeng and Wang, Jianlin and Wang, Rutong and Guo, Yongqi and Zhao, Liqiang}, journal={Expert Systems with Applications}, volume={182}, pages={115223}, year={2021}, publisher={Elsevier} } ``` ## How to use ### 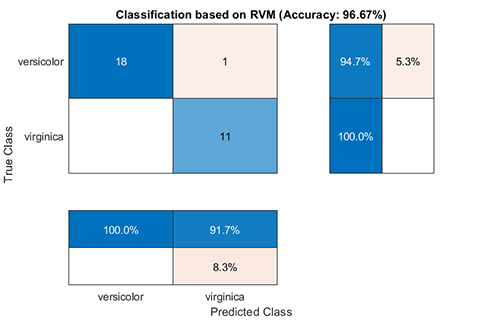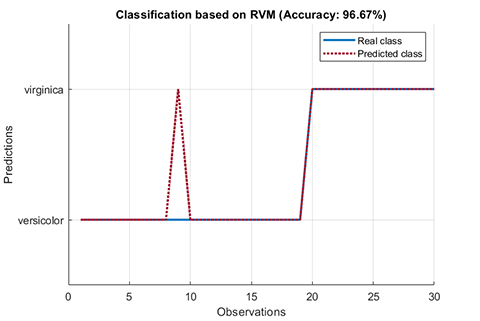01. Classification using RVM (RVC) A demo for classification using RVM ``` clc clear all close all addpath(genpath(pwd)) % use fisheriris dataset load fisheriris inds = ~strcmp(species, 'setosa'); data_ = meas(inds, 3:4); label_ = species(inds); cvIndices = crossvalind('HoldOut', length(data_), 0.3); trainData = data_(cvIndices, :); trainLabel = label_(cvIndices, :); testData = data_(~cvIndices, :); testLabel = label_(~cvIndices, :); % kernel function kernel = Kernel('type', 'gaussian', 'gamma', 0.2); % parameter parameter = struct( 'display', 'on',... 'type', 'RVC',... 'kernelFunc', kernel); rvm = BaseRVM(parameter); % RVM model training, testing, and visualization rvm.train(trainData, trainLabel); results = rvm.test(testData, testLabel); rvm.draw(results) ``` results: ``` *** RVM model (classification) train finished *** running time = 0.1604 seconds iterations = 20 number of samples = 70 number of RVs = 2 ratio of RVs = 2.8571% accuracy = 94.2857% *** RVM model (classification) test finished *** running time = 0.0197 seconds number of samples = 30 accuracy = 96.6667% ```

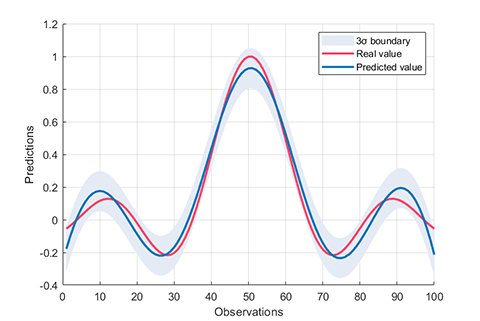
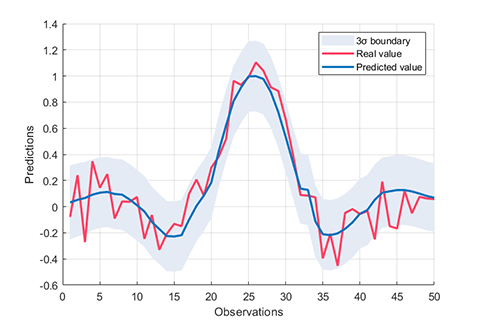
### 02. Regression using RVM (RVR) A demo for regression using RVM ``` clc clear all close all addpath(genpath(pwd)) % sinc funciton load sinc_data trainData = x; trainLabel = y; testData = xt; testLabel = yt; % kernel function kernel = Kernel('type', 'gaussian', 'gamma', 0.1); % parameter parameter = struct( 'display', 'on',... 'type', 'RVR',... 'kernelFunc', kernel); rvm = BaseRVM(parameter); % RVM model training, testing, and visualization rvm.train(trainData, trainLabel); results = rvm.test(testData, testLabel); rvm.draw(results) ``` results: ``` *** RVM model (regression) train finished *** running time = 0.1757 seconds iterations = 76 number of samples = 100 number of RVs = 6 ratio of RVs = 6.0000% RMSE = 0.1260 R2 = 0.8821 MAE = 0.0999 *** RVM model (regression) test finished *** running time = 0.0026 seconds number of samples = 50 RMSE = 0.1424 R2 = 0.8553 MAE = 0.1106 ```

### 03. Kernel funcions A class named ***Kernel*** is defined to compute kernel function matrix. ``` %{ type - linear : k(x,y) = x'*y polynomial : k(x,y) = (γ*x'*y+c)^d gaussian : k(x,y) = exp(-γ*||x-y||^2) sigmoid : k(x,y) = tanh(γ*x'*y+c) laplacian : k(x,y) = exp(-γ*||x-y||) degree - d offset - c gamma - γ %} kernel = Kernel('type', 'gaussian', 'gamma', value); kernel = Kernel('type', 'polynomial', 'degree', value); kernel = Kernel('type', 'linear'); kernel = Kernel('type', 'sigmoid', 'gamma', value); kernel = Kernel('type', 'laplacian', 'gamma', value); ``` For example, compute the kernel matrix between **X** and **Y** ``` X = rand(5, 2); Y = rand(3, 2); kernel = Kernel('type', 'gaussian', 'gamma', 2); kernelMatrix = kernel.computeMatrix(X, Y); >> kernelMatrix kernelMatrix = 0.5684 0.5607 0.4007 0.4651 0.8383 0.5091 0.8392 0.7116 0.9834 0.4731 0.8816 0.8052 0.5034 0.9807 0.7274 ``` ### 04. Hybrid kernel A demo for regression using RVM with hybrid_kernel (K =w1×K1+w2×K2+...+wn×Kn) ``` clc clear all close all addpath(genpath(pwd)) % sinc funciton load sinc_data trainData = x; trainLabel = y; testData = xt; testLabel = yt; % kernel function kernel_1 = Kernel('type', 'gaussian', 'gamma', 0.3); kernel_2 = Kernel('type', 'polynomial', 'degree', 2); kernelWeight = [0.5, 0.5]; % parameter parameter = struct( 'display', 'on',... 'type', 'RVR',... 'kernelFunc', [kernel_1, kernel_2],... 'kernelWeight', kernelWeight); rvm = BaseRVM(parameter); % RVM model training, testing, and visualization rvm.train(trainData, trainLabel); results = rvm.test(testData, testLabel); rvm.draw(results) ``` ### 05. Parameter Optimization for single-kernel-RVM A demo for RVM model with Parameter Optimization ``` clc clear all close all addpath(genpath(pwd)) % use fisheriris dataset load fisheriris inds = ~strcmp(species, 'setosa'); data_ = meas(inds, 3:4); label_ = species(inds); cvIndices = crossvalind('HoldOut', length(data_), 0.3); trainData = data_(cvIndices, :); trainLabel = label_(cvIndices, :); testData = data_(~cvIndices, :); testLabel = label_(~cvIndices, :); % kernel function kernel = Kernel('type', 'gaussian', 'gamma', 5); % parameter optimization opt.method = 'bayes'; % bayes, ga, pso opt.display = 'on'; opt.iteration = 20; % parameter parameter = struct( 'display', 'on',... 'type', 'RVC',... 'kernelFunc', kernel,... 'optimization', opt); rvm = BaseRVM(parameter); % RVM model training, testing, and visualization rvm.train(trainData, trainLabel); results = rvm.test(trainData, trainLabel); rvm.draw(results) ``` results: ``` *** RVM model (classification) train finished *** running time = 13.3356 seconds iterations = 88 number of samples = 70 number of RVs = 4 ratio of RVs = 5.7143% accuracy = 97.1429% Optimized parameter table gaussian_gamma ______________ 7.8261 *** RVM model (classification) test finished *** running time = 0.0195 seconds number of samples = 70 accuracy = 97.1429% ```

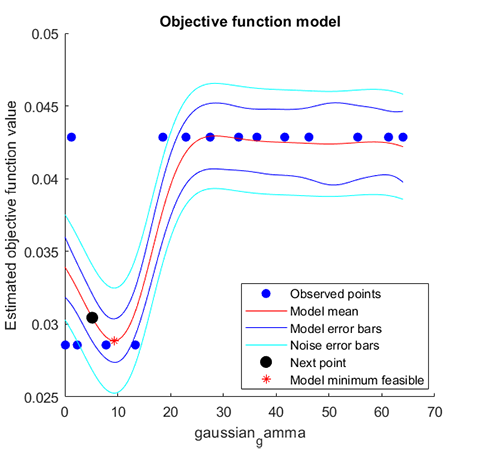
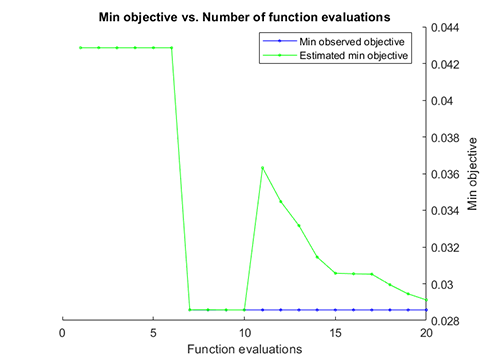
### 06. Parameter Optimization for hybrid-kernel-RVM A demo for RVM model with Parameter Optimization ``` %{ A demo for hybrid-kernel RVM model with Parameter Optimization %} clc clear all close all addpath(genpath(pwd)) % data load UCI_data trainData = x; trainLabel = y; testData = xt; testLabel = yt; % kernel function kernel_1 = Kernel('type', 'gaussian', 'gamma', 0.5); kernel_2 = Kernel('type', 'polynomial', 'degree', 2); % parameter optimization opt.method = 'bayes'; % bayes, ga, pso opt.display = 'on'; opt.iteration = 30; % parameter parameter = struct( 'display', 'on',... 'type', 'RVR',... 'kernelFunc', [kernel_1, kernel_2],... 'optimization', opt); rvm = BaseRVM(parameter); % RVM model training, testing, and visualization rvm.train(trainData, trainLabel); results = rvm.test(testData, testLabel); rvm.draw(results) ``` results: ``` *** RVM model (regression) train finished *** running time = 24.4042 seconds iterations = 377 number of samples = 264 number of RVs = 22 ratio of RVs = 8.3333% RMSE = 0.4864 R2 = 0.7719 MAE = 0.3736 Optimized parameter 1×6 table gaussian_gamma polynomial_gamma polynomial_offset polynomial_degree gaussian_weight polynomial_weight ______________ ________________ _________________ _________________ _______________ _________________ 22.315 13.595 44.83 6 0.042058 0.95794 *** RVM model (regression) test finished *** running time = 0.0008 seconds number of samples = 112 RMSE = 0.7400 R2 = 0.6668 MAE = 0.4867 ```

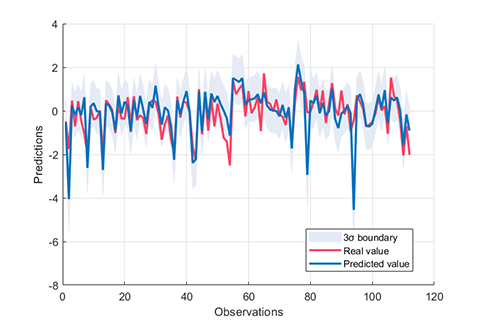
### 07. Cross Validation In this code, two cross-validation methods are supported: 'K-Folds' and 'Holdout'. For example, the cross-validation of 5-Folds is ``` parameter = struct( 'display', 'on',... 'type', 'RVC',... 'kernelFunc', kernel,... 'KFold', 5); ``` For example, the cross-validation of the Holdout method with a ratio of 0.3 is ``` parameter = struct( 'display', 'on',... 'type', 'RVC',... 'kernelFunc', kernel,... 'HoldOut', 0.3); ``` ### 08. Other option ``` %% custom optimization option %{ opt.method = 'bayes'; % bayes, ga, pso opt.display = 'on'; opt.iteration = 20; opt.point = 10; % gaussian kernel function opt.gaussian.parameterName = {'gamma'}; opt.gaussian.parameterType = {'real'}; opt.gaussian.lowerBound = 2^-6; opt.gaussian.upperBound = 2^6; % laplacian kernel function opt.laplacian.parameterName = {'gamma'}; opt.laplacian.parameterType = {'real'}; opt.laplacian.lowerBound = 2^-6; opt.laplacian.upperBound = 2^6; % polynomial kernel function opt.polynomial.parameterName = {'gamma'; 'offset'; 'degree'}; opt.polynomial.parameterType = {'real'; 'real'; 'integer'}; opt.polynomial.lowerBound = [2^-6; 2^-6; 1]; opt.polynomial.upperBound = [2^6; 2^6; 7]; % sigmoid kernel function opt.sigmoid.parameterName = {'gamma'; 'offset'}; opt.sigmoid.parameterType = {'real'; 'real'}; opt.sigmoid.lowerBound = [2^-6; 2^-6]; opt.sigmoid.upperBound = [2^6; 2^6]; %} %% RVM model parameter %{ 'display' : 'on', 'off' 'type' : 'RVR', 'RVC' 'kernelFunc' : kernel function 'KFolds' : cross validation, for example, 5 'HoldOut' : cross validation, for example, 0.3 'freeBasis' : 'on', 'off' 'maxIter' : max iteration, for example, 1000 %} ```