# ImPro
**Repository Path**: linux_search/im-pro
## Basic Information
- **Project Name**: ImPro
- **Description**: 帮数图老师写的数字图像处理实验平台。
基于pyside2
- **Primary Language**: Python
- **License**: LGPL-3.0
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 1
- **Created**: 2024-09-02
- **Last Updated**: 2024-09-02
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# ImPro
#### 介绍
用python3和PySide2写的图像处理平台
#### 使用说明
需要先安装Python3,然后通过Python包管理工具安装`numpy`、`Pillow`、`PySide2`
注意。Python3的版本不要低于3.7(写的时候用的3.7,更低的没用过),不要高于3.9(3.10似乎不支持PySide2了)
UI_MainWindow.py是应用的表现层,是图形界面的类。
Func.py是函数具体的算法实现。
main.py是程序入口,将图像界面和函数功能相关联。
待填空版只需完成Func.py中的各函数功能的即可。
##### 1.图像读取
读取.raw格式的图片,有两种方法。
- 直接读取文件,读取后返回值是“字节流”,前八个字节调用python的标准库struct的unpack方法解析为unsigned int型,得到图像的宽和高,八个字节之后的逐字节存入一个数组,由于python没有指针,所以最后记得返回dst,实现方法如下:
```python
def read_raw(path):
with open(path, 'rb') as f:
data = f.read()
# data是一个python中的一种特殊的字符串,叫做“字节流”,每一个单元就是一个字节
w_byte = data[:4] # 前四个字节是图片的宽 读取出来是 b'\x80\x01\x00\x00' 等于 0*1+8*16+1*256 = 384
h_byte = data[4:8] # 第5-8字节是图片的高
im = data[8:] # 第8个字节以后才是图像的像素灰度值,一个灰度值刚好是一个字节
w = struct.unpack('I', w_byte)[0] # 将四个字节的字节流转换为无符号整型
h = struct.unpack('I', h_byte)[0]
dst = np.zeros((h, w), dtype=np.uint8) # 创建一个h x w 的全零矩阵dst,所有元素都是8位无符号整型,也就是0-255
for i in range(h):
for j in range(w):
dst[i][j] = im[i*w + j] # 将im中的灰度值逐个存入dst
return dst
```
- 调用numpy库的fromfile方法,按照指定的数据类型读取文件,由于像素和宽高数据的数据类型不同,所以要先用np.uint32,再用np.uint8,raw格式的图片前8个字节分别是图片的宽和高,各占4个字节(Byte)即32位(bit),计算机存储数据时,存储的就是一连串的二进制数字0/1,np.uint32就是32个连续的二进制数据为一个数据,读出来的十进制数字无符号,在0到$2^{32}$的范围内,用numpy按照np.uint32去读取数据后,截取前2位就是宽和高了,但是在这之后,不能直接用astype(np.uint8)转换数据类型,因为读取之后数组大小定了,再转换也只是数组的每一个数字模256(除以256然后取余数)了,所以要重新再以np.uint8读取数据这个时候,之前的宽和高被分成了8个数字,略去这前8个数字,后面的都是像素的灰度级
```python
def read_raw(path):
w, h = np.fromfile(path, dtype=np.uint32)[:2]
dst = np.fromfile(path, dtype=np.uint8)[8:]
dst = dst.reshape(h, w)
return dst
```
Qt中所有显示出来的东西,都需要一个QWidget类作为依托,QPushButton、QLabel等本身继承自QWidget,可以直接显示,图片通常是QImage或者QPixmap,需要一个QWidget去承载,而QLabel刚好可以装载图片,所以笔者用三个QLabel(分别命名为label_src,label_dst,label_ext)作为装载图片的容器,如果有更多的图片要显示,可以在UI_MainWindow.py中添加,添加后要move到一个位置,否则挡住菜单栏使用不了。
这里给出一种测试可用的方法,更多用法见https://doc.qt.io/qt-5/classes.html,读者可自行探索。
```python
# 显示图像,image为图像像素灰度的矩阵,label为用于装载图片的组件,x, y为label在界面的位置
def show_image(image, label, x, y):
h, w = image.shape[:2]
qimg = QImage(w, h, QImage.Format_RGB32)
# 彩色图像
if image.ndim == 3:
for i in range(h):
for j in range(w):
val = qRgb(image[i][j][0], image[i][j][1], image[i][j][2]) # rgb
qimg.setPixel(j, i, val)
# 灰度图像
elif image.ndim == 2:
for i in range(h):
for j in range(w):
val = qRgb(image[i][j], image[i][j], image[i][j])
qimg.setPixel(j, i, val)
pixmap = QPixmap.fromImage(qimg)
label.setPixmap(pixmap)
label.setGeometry(x, y, w, h)
label.show()
label.raise_() # 置于最上层
```
##### 2.图像直方图
这一部分分为两步,分别是直方图的计算和合理地显示直方图。
首先了解,图像的灰度直方图的概念。在我们小学或中学阶段或多或少的了解过一些统计的知识,例如统计班级中各个分数段的人数,然后绘制成一个柱状图,这就是我们最早接触到的直方图,类似地,图像灰度直方图就是统计图像各个灰度级上像素灰度个数的统计图,以直方图形式呈现。
于是我们可以设计程序将图像各个灰度级上的像素个数计算出来:
```python
# 计算直方图
def cal_hist(src):
hist = np.zeros(256, dtype=int) # 先赋值一个全零数组,用来统计各个灰度级像素个数
h, w = src.shape[:2] # 取图像矩阵的高和宽
for i in range(h):
for j in range(w):
hist[src[i][j]] += 1 # 统计
return hist
```
接着就是要合理的显示直方图,何为合理?就是至少得让直方图完整的呈现在图形界面上面,不会有显示不完全的情况,所以就要限制直方图的上界,对于Qt,所有图像都需要一个组件来装载,这个组件在界面中大小是有限的,取决于传入的图像矩阵的宽和高,以及界面大小,所以预先取$1024 \times 400$,1024刚好是256的4倍,是为了绘制直方图时留出一定间隙,400为图像的高,因此需要将最大值对应此高度,将直方图标准化到0-400的范围,下面是生成直方图的程序:
```python
# 绘制直方图的图像
def plot_hist(src):
hist = cal_hist(src)
# 直方图单独看作一张图片,设置其高度为400px,宽度为1024px,即为256的4倍,这样能够显示出一条条分立的谱线
img_h = 400
img_w = 256 * 4
max_val = hist.max()
if max_val == 0:
max_val = 1000000
coeffs = (400 - 20) / max_val # 直方图归一化,减20是为了不到顶
normed_hist = hist * coeffs
normed_hist = normed_hist.astype(int)
dst = np.ones((img_h, img_w), dtype=np.uint8) + 254 # 用于保存直方图的图片的矩阵,全白
for i in range(img_w >> 2): # 右移两位,相当于除以4
for j in range(img_h, 0, -1):
if j < normed_hist[i]:
dst[400 - j][i << 2] = 0
return dst
```
新建一个400 x 1024的数组,每个值都为255,相当于一张纯白的图片;将直方图的最小值到最大值映射到0~400的范围;将对应的位置设为0,即黑色。`400-20`是为了图像上方不到顶,求max_val直接调用了numpy数组自带的方法,也可以通过通过下面的方法求出,时间复杂度`O(n)`。
```python
max_val = 1
for i in range(len(hist)):
if hist[i] > max_val:
max_val = hist[i]
```
由于`i,j,img_w,img_h`都是整数,所以用移位运算`<<`和`>>`代替乘除法(逻辑移位),提高运算效率(python中只要做除法,就会自动转换成浮点运算),右移一位相当于除以2,左移一位相当于乘以2,其原理如下
```
img_w = 1024 = 2^10 = 10000000000
img_w >> 2 = 00100000000 = 2^8 = 256 右移高位补零,左移低位补零
```
最终显示直方图如下
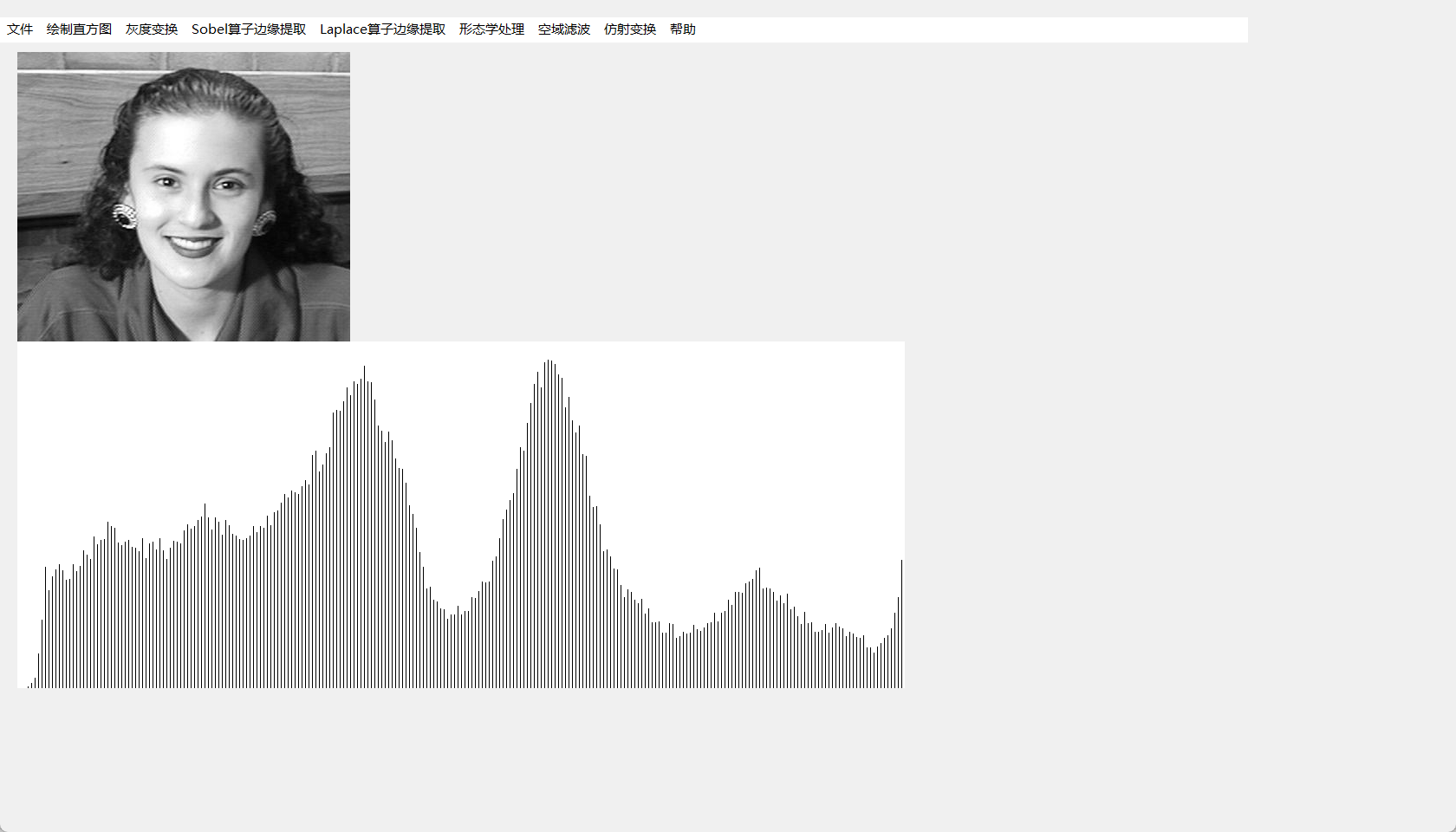
当然,在Qt中也可以使用matplotlib库或者pyqtgraph绘制直方图,但是绘制出来的图像多少有些违和(如下图所示)。
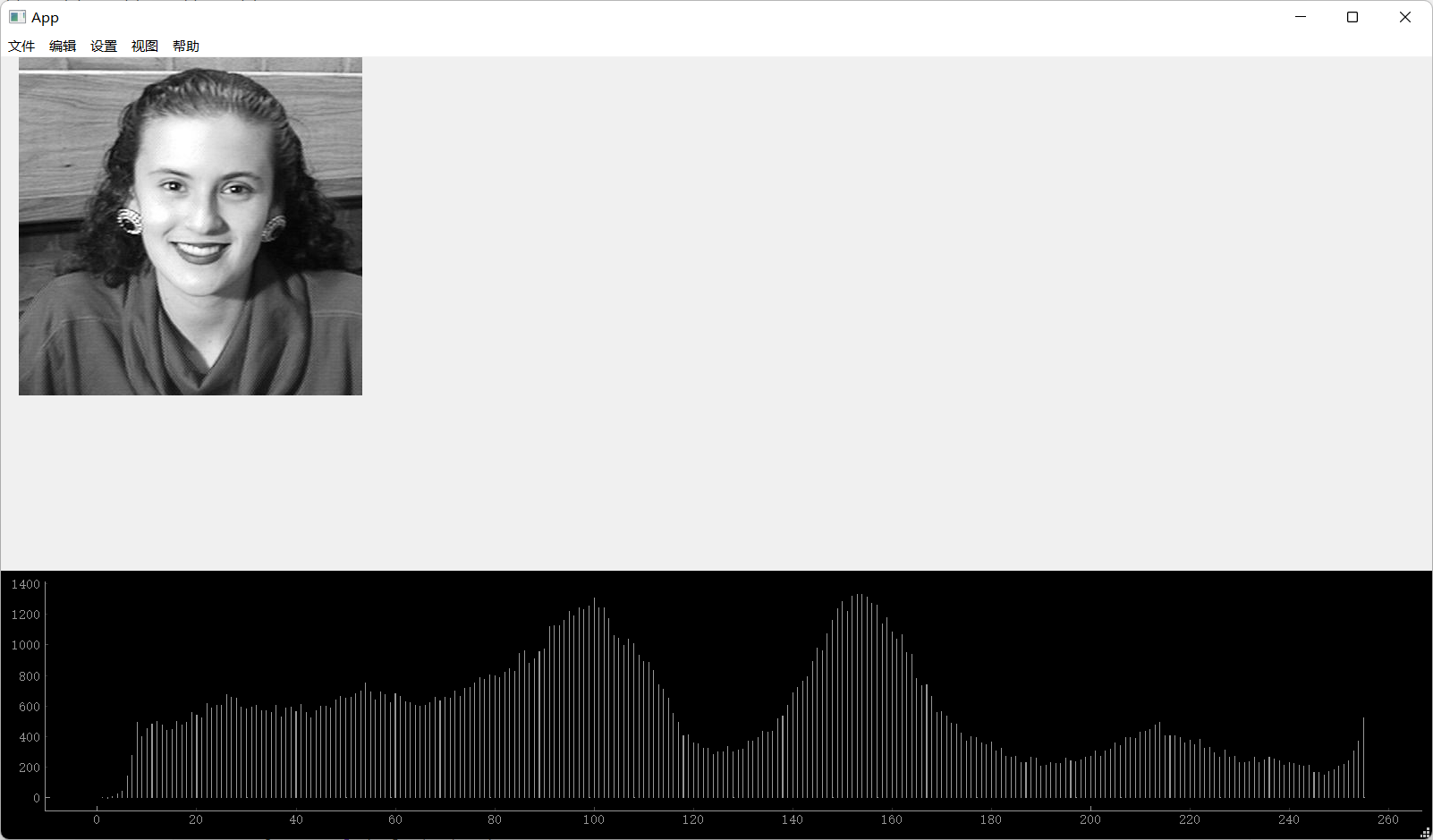
使用pyqtgraph在Qt程序中绘制直方图
##### 3.灰度变换
灰度变换是空间域增强的常用方法之一,是直接对构成图像像素的灰度级操作。具体操作是通过灰度变换函数,将输入图像的像素灰度值,转换成另一种灰度值。根据灰度变换函数的线性性,可将灰度变换分为线性变换和非线性变换,由于图像不同灰度区间上的信息对人们的重要程度不同,往往我们需要突出感兴趣的区间,抑制不感兴趣的区间,这就要求对不同区间有着不同的特性(突出或者抑制),所以非线性变换的使用较多,下面介绍几种常见的灰度变换方法。
- 二值化
二值化常用于分割目标和背景,这里只实现简单的、给定阈值的二值化,后续在图像分割再介绍其他二值化方法
```python
# 二值化
def binarize(src, th):
h, w = src.shape[:2]
dst = np.zeros_like(src)
for i in range(h):
for j in range(w):
if src[i][j] > th:
dst[i][j] = 255
return dst
```
这里传入两个参数,一个是待处理的图像矩阵,另一个是灰度阈值,新构造了一个全零矩阵,大于该阈值的像素的灰度重置为255,实验效果如下:
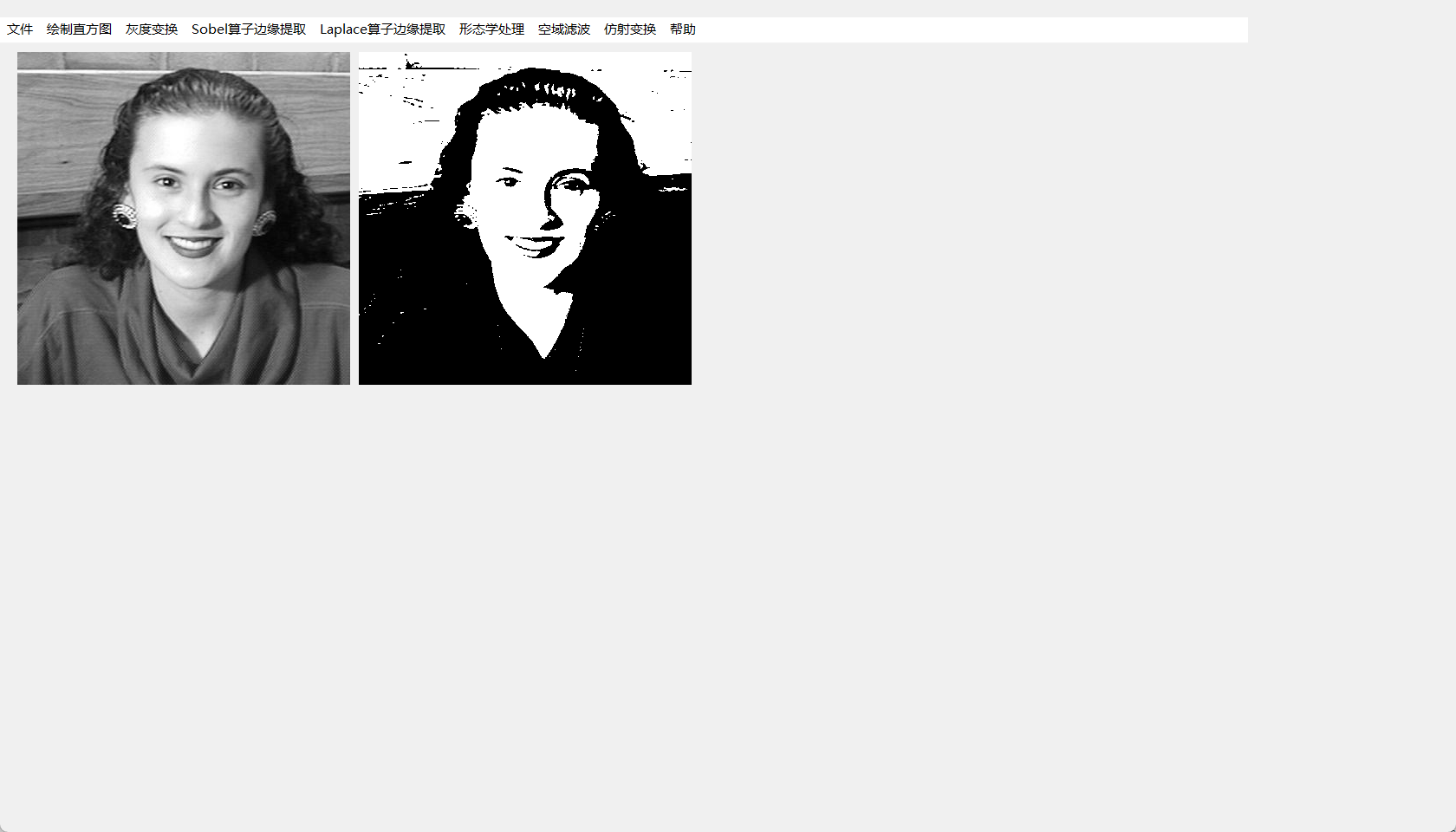
- 对数变换
对数变换的表达式为$s = c \times log(1+r)$,这里取c = 1,可以画出其图像
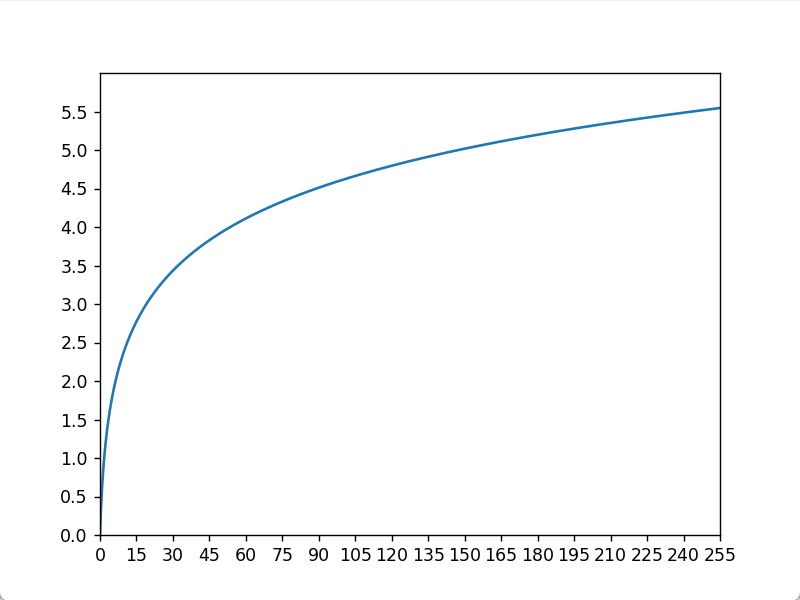
可以看到,变换后的灰度范围不再是`0~255`了,所以还要将其映射到`0~255`的范围,如下
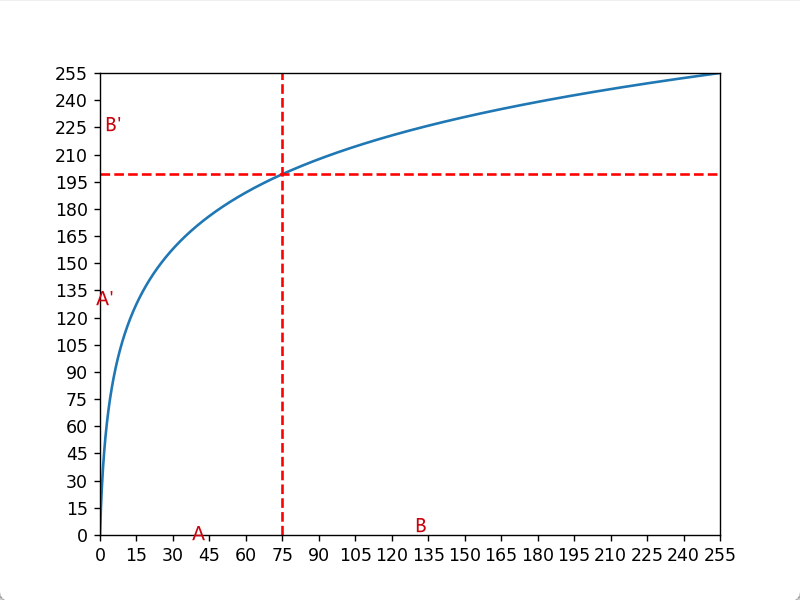
如图所示,灰度区间`A`的对应变换后的`A'`,`B`对应`B'`,可以看出`A`的动态范围得到了拉伸,`B`的动态范围被压缩,也就是说,图像的暗部向往高灰度即挪动了,图像整体变亮了。
换一种思路思考图像经过灰度变换之后的明暗变化,从微观上来讲,例如对于原图像中像素值为75的一个或几个像素点,其变换后图像的像素值为198,灰度值增大了,当我们观察曲线上的其他点,也同样得出这个结论,所以说,图像整体是变亮了;从宏观上来看,我们假定原图像各灰度级上的像素个数均匀分布,由于区间`B`大于`A`,所以`B`包含的像素个数大于`A`,变换后,将`B`中的像素分布集中到一个高灰度的窄区间,我们也可以从其直方图看出端倪:
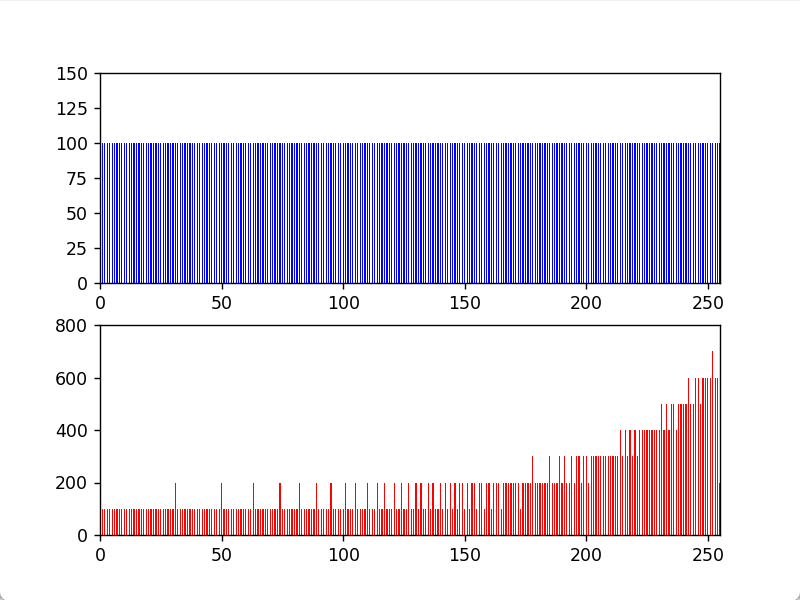
下面是其python实现
```python
# 对数变换
def log_trans(src):
dst = np.zeros_like(src)
data = src.astype(np.float16) # 先转换数据类型,因为对数运算会产生小数
tmp = np.log(data + 1) # numpy数组的广播特性,所有元素+1再取对数
coeffs = 255 / tmp.max()
tmp = tmp * coeffs
dst = tmp.astype(np.uint8)
return dst
```
效果如下
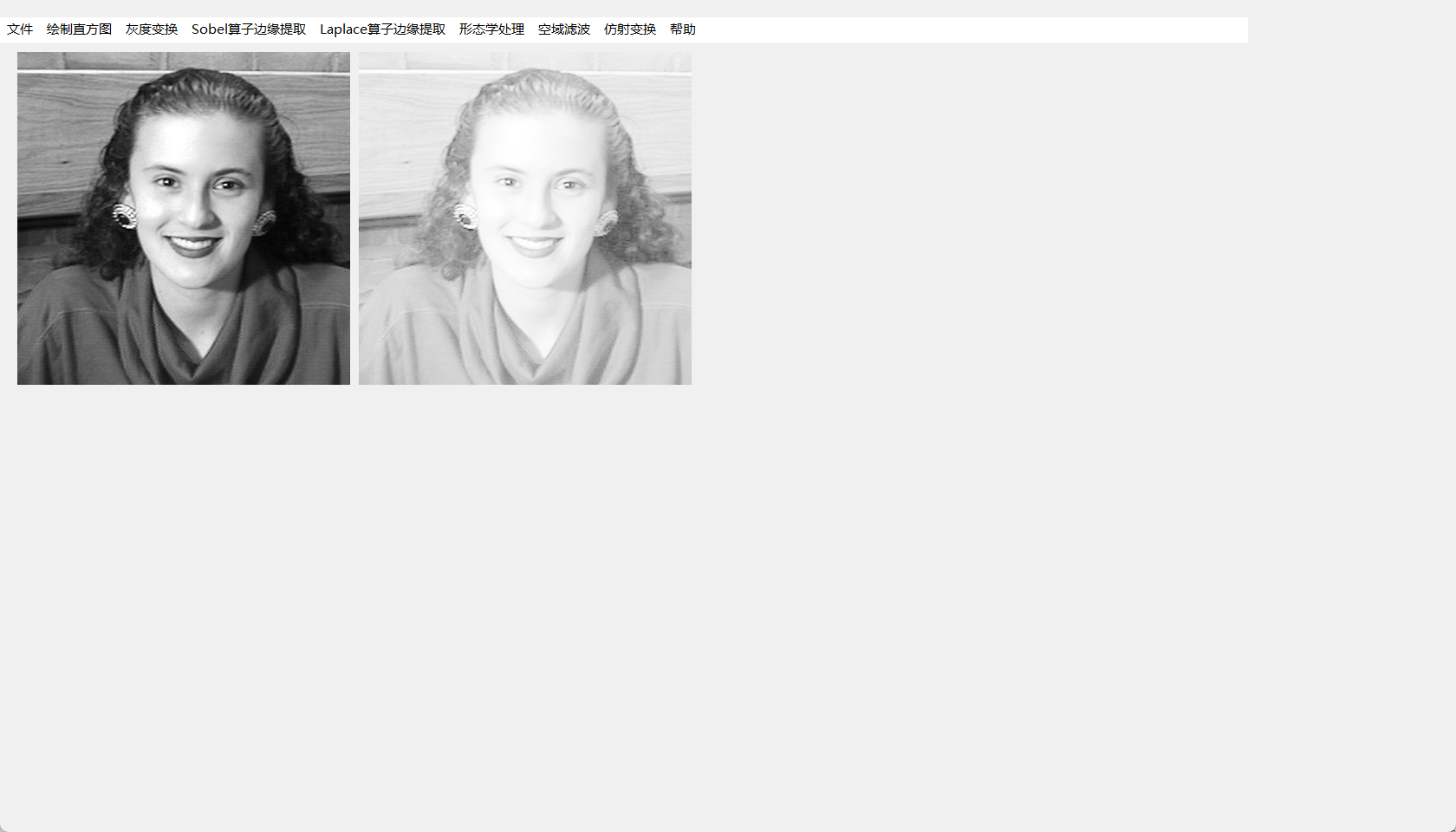
- 幂次变换
幂次变换又称指数变换,其表达式为$s = c \times r^{\gamma}$,取`c = 1`,当$\gamma \gt 1$,其其图像如下
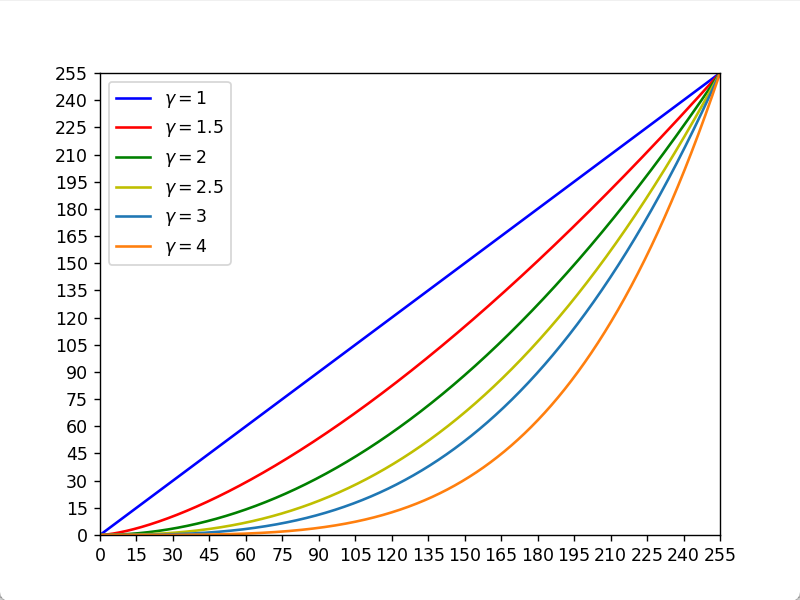
不难得出,原图像经过上图所示的函数对应的变换后,整体变暗了。
python实现如下:
```python
# 幂次变换
def exp_trans(src, expon):
data = src.astype(np.float64) # 先转换数据类型
tmp = np.power(data, expon)
coeffs = 255 / tmp.max()
tmp = tmp * coeffs
dst = tmp.astype(np.uint8)
return dst
```
变换后的效果如下:
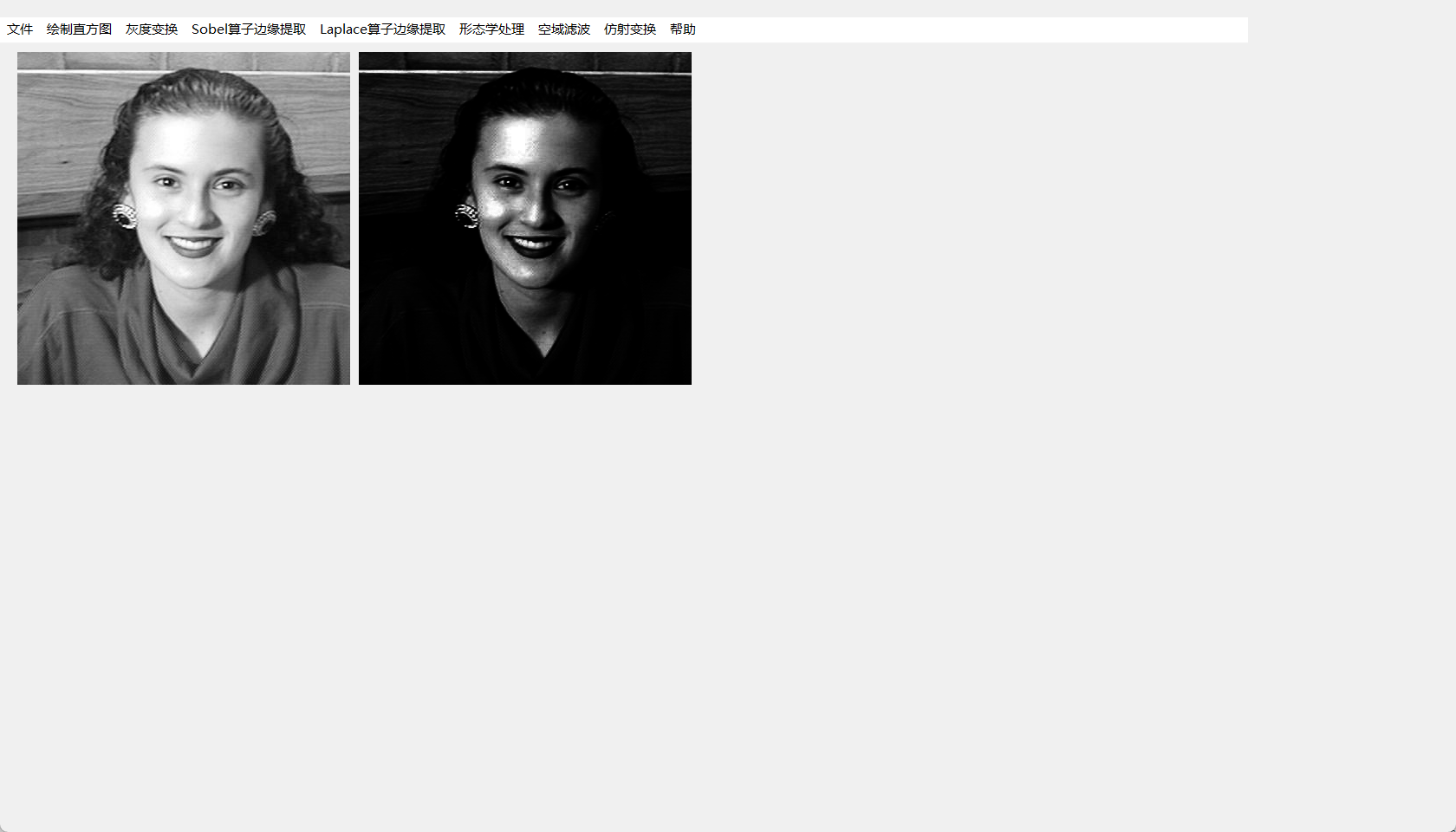
$\gamma \lt 1$ 时,其图像如下
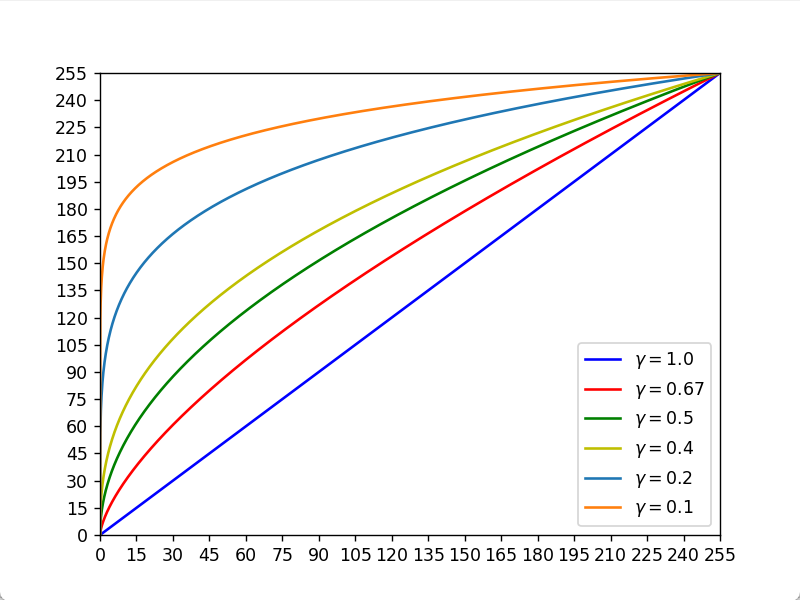
该图像与对数变换的图像很相似,作用也相似,能将图像整体变亮。
##### 4.直方图均衡
灰度直方图是图像灰度的统计特征,直方图均衡和其他灰度变换类似,只不过幂次变换的灰度变换函数是指数函数$s = c \times r^{\gamma}$,对数变换的灰度变换函数是对数函数$s = c \times log(1+r)$,二值化的变换函数是一个符号函数,直方图均衡的变换函数是灰度级的累积分布函数,一般是一条斜率先增大后减小的曲线(大多数图像中等的灰度级多),即两头的斜率小(一般比1小),中间的斜率大(一般比1大),于是经过这个函数的变换之后,极暗或者极亮的部分动态范围被压缩,亮度适宜的部分动态范围被拉伸。
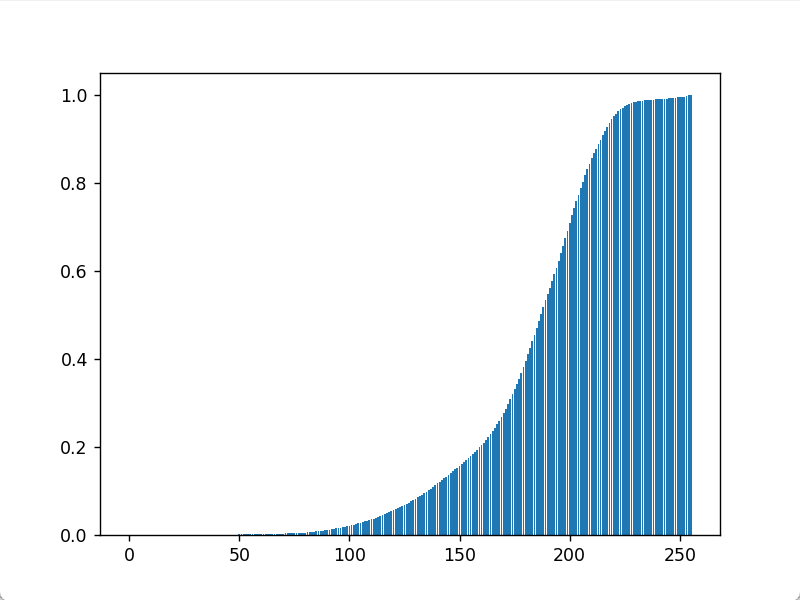
FILE16.raw的累积分布直方图
当然,也不是所有的图像的累计分布直方图都是这样的形态,但是图像的直方图越趋近均匀分布,就越是这样,而使得图像的像素个数在各个灰度级上均匀分布,正是直方图均衡的目的。对于其他更一般的直方图,在像素个数突增的部分,累积分布函数斜率较大,经过直方图均衡后,这一部分的动态范围被拉伸,这些像素分布到比原先更大的范围,对应到直方图里面就是直方图的峰变得缓和;同理,在像素个数增加缓慢的区域,这一部分区间的动态范围被压缩,对应到直方图上就是像素个数少的灰度级相互合并,像素个数增加,我们可以通过下图更直观的感受直方图均衡带来的效果:
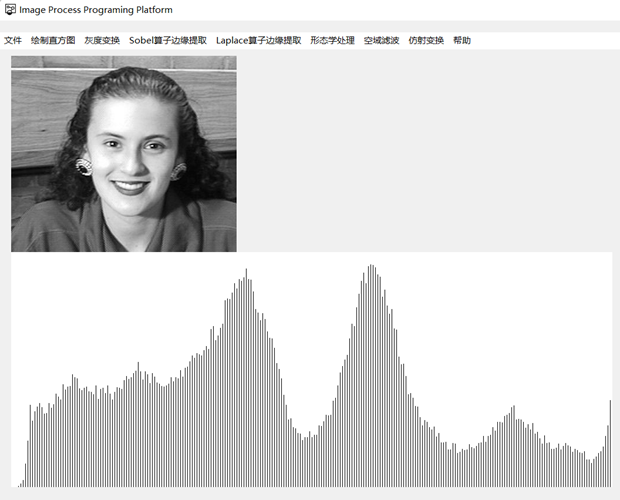
FILE1.raw直方图均衡前
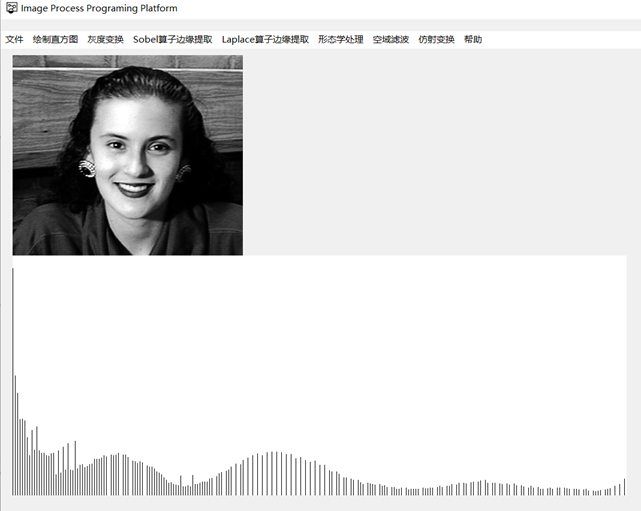
FILE1.raw直方图均衡后
直方图均衡的python实现
```python
# 计算直方图
def cal_hist(src):
hist = np.zeros(256, dtype=int) # 先赋值一个全零数组,用来统计各个灰度级像素个数
h, w = src.shape[:2] # 取图像矩阵的高和宽
for i in range(h):
for j in range(w):
hist[src[i][j]] += 1 # 统计
return hist
# 直方图均衡
def hist_eql(src):
h, w = src.shape[:2]
# 计算直方图
hist = cal_hist(src)
# 求概率密度直方图
hist_pdf = hist.astype(np.float32)
hist_pdf = hist_pdf / hist_pdf.sum() # 归一化
# 求累积分布直方图
hist_cdf = np.zeros(256, dtype=np.float32)
hist_cdf[0] = hist_pdf[0]
for i in range(1, 256):
hist_cdf[i] = hist_pdf[i] + hist_cdf[i - 1]
coeffs = np.arange(0, 256)
hist_map = hist_cdf * coeffs # 求旧灰度级到新灰度级之间的映射,两个数组形状相同,对应位置相乘
dst = np.zeros_like(src)
for i in range(h):
for j in range(w):
dst[i][j] = hist_map[src[i][j]]
return dst
```
##### 5.空域滤波
这里主要介绍两种低通滤波器——均值、高斯低通滤波器和一种排序统计滤波器——中值滤波器
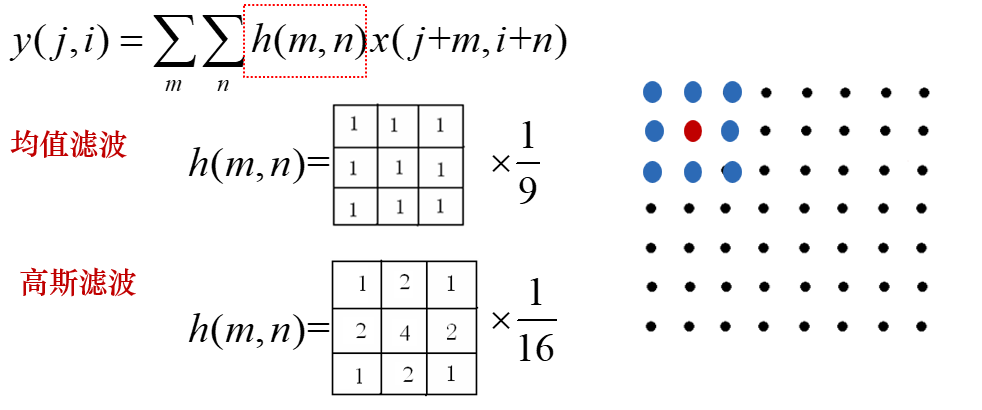
均值滤波器和高斯滤波器能够有效的将噪声点的能量平均到其8邻域的各个像素上。
中值滤波器能够取8邻域像素灰度的中位数,能够避免椒盐噪声这样的极端值的影响。
**均值滤波器**
```python
# 均值滤波 不考虑图像最外的一圈像素
def mean_filter(src):
h, w = src.shape[:2]
dst = np.zeros((h, w), dtype=np.uint8)
for i in range(1, h-1):
for j in range(1, w-1):
block = src[i-1:i+2, j-1:j+2]
dst[i][j] = int(block.mean()) # numpy数组的方法mean,返回平均值
return dst
```
这样处理固然也可以,但是图像最外层的像素信息丢失掉了,所以考虑将图像看作在空间上是周期的:

改良之后:
```python
# 均值滤波
def mean_filter(src):
h, w = src.shape[:2]
# 将待处理的基础图像扩展一圈,使得边缘处的像素点也可以被遍历到
tmp = np.zeros((h + 2, w + 2), dtype=np.uint8)
dst = np.zeros((h, w), dtype=np.uint8)
tmp[1:-1, 1:-1] = copy.deepcopy(src)
tmp[:, -1] = tmp[:, 1]
tmp[:, 0] = tmp[:, -2]
tmp[-1, :] = tmp[1, :]
tmp[0, :] = tmp[-2, :]
for i in range(h):
for j in range(w):
block = src[i:i + 3, j:j + 3]
dst[i][j] = int(block.mean()) # numpy数组的方法mean,返回平均值
return dst
```
**高斯滤波器**
```python
# 高斯滤波
def gaussian_filter(src):
h, w = src.shape[:2]
kernel = np.array([[1, 2, 1],
[2, 4, 2],
[1, 2, 1]])
# 将待处理的基础图像扩展一圈,使得边缘处的像素点也可以被遍历到
tmp = np.zeros((h + 2, w + 2), dtype=np.uint8)
dst = np.zeros((h, w), dtype=np.uint8)
tmp[1:-1, 1:-1] = copy.deepcopy(src)
tmp[:, -1] = tmp[:, 1]
tmp[:, 0] = tmp[:, -2]
tmp[-1, :] = tmp[1, :]
tmp[0, :] = tmp[-2, :]
for i in range(h):
for j in range(w):
block = tmp[i:i + 3, j:j + 3] * kernel
dst[i][j] = block.sum() >> 4 # 右移4位即除以16,移位运算比浮点数除法快
return dst
```
这里使用了`>>4`来代替`/16`,因为python在做除法运算时会自动将数据转换为浮点型,效率较低,使用移位运算效率高。
**中值滤波器**
```python
# 中值滤波
def median_filter(src):
h, w = src.shape[:2]
# 将待处理的基础图像扩展一圈,使得边缘处的像素点也可以被遍历到
tmp = np.zeros((h + 2, w + 2), dtype=np.uint8) # 在原图像的基础上构造一个比它大一圈的图像
dst = np.zeros((h, w), dtype=np.uint8)
tmp[1:-1, 1:-1] = copy.deepcopy(src) # 这个大一圈的矩阵除去边缘之外的值赋值为原图像
tmp[:, -1] = tmp[:, 1] # 用原图像的第1行(tmp的第2行)补到tmp的最后一行
tmp[:, 0] = tmp[:, -2] # 用原图像的最后1行(tmp的倒数第2行)补到tmp的第1行
tmp[-1, :] = tmp[1, :]
tmp[0, :] = tmp[-2, :]
for i in range(h):
for j in range(w):
block = tmp[i:i + 3, j:j + 3].reshape(-1)
block.sort() # numpy的sort方法,排序
dst[i][j] = block[len(block) // 2] # 返回中位数
return dst
```
##### 6.边缘提取
一阶: Roberts算子、Sobel算子、Prewitt算子、Kirsch算子、Robinson算子
二阶: Laplacian算子、Canny算子、Marr-Hildreth(LoG算子)
这里只介绍Sobel算子
```python
sob_x = np.array([[-1, 0, 1], # 水平方向
[-2, 0, 2],
[-1, 0, 1]])
sob_y = np.array([[-1, -2, -1], # 垂直方向
[0, 0, 0],
[1, 2, 1]])
```
python实现如下:
```python
# sobel算子边缘提取
def sobel(src):
sob_x = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
sob_y = np.array([[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]])
h, w = src.shape[:2]
# 构造与src同形状的零矩阵
sobel_x = np.zeros_like(src)
sobel_y = np.zeros_like(src)
for i in range(1, h - 1):
for j in range(1, w - 1):
mask = src[i - 1:i + 2, j - 1:j + 2] # 切片操作,取(i, j)为中心,3 x 3的一个小方框(8邻域)
sobel_x[i][j] = np.abs((sob_x * mask).sum())
sobel_y[i][j] = np.abs((sob_y * mask).sum())
return sobel_x, sobel_y
```
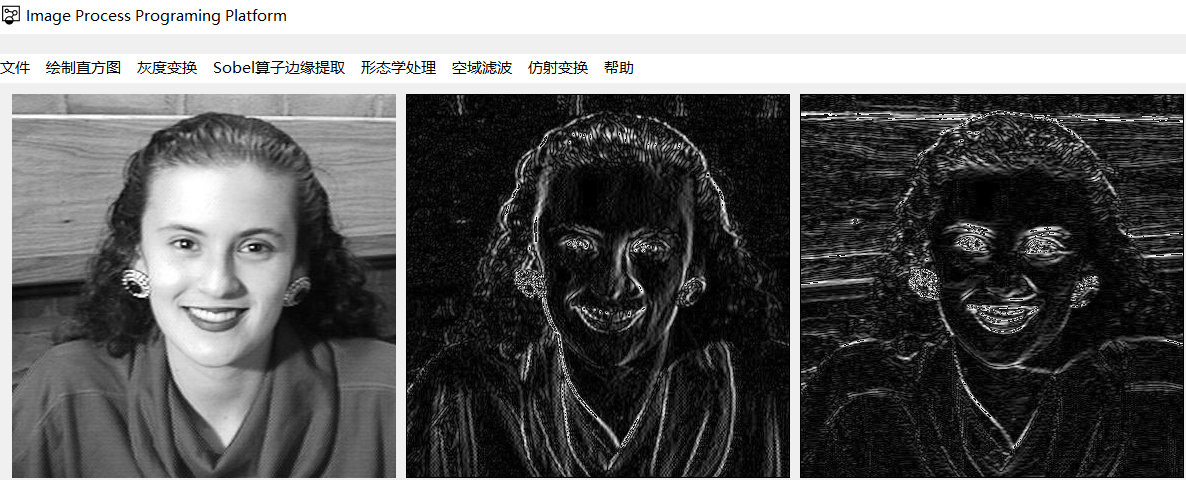
Sobel算子边缘提取原图(左)、水平方向边缘(中)、垂直方向边缘(右)
##### 7.形态学处理
腐蚀和膨胀是两种最基本也是最重要的形态学运算, 它们是很多高级形态学处理的基础, 很多其他的形态学算法都是由这两种基本运算复合而成。
**结构元素**
结构元素在算子参数中的名称为 StructElement,在腐蚀与膨胀操作中都需要用到。结构元素是类似于“滤波核”的元素,或者说类似于一个“小窗”,在原图上进行“滑动”,这就是结构元素。
```python
# 结构元素
MORPH_CROSS = np.array([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]], int)
MORPH_RECT = np.array([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]], int)
```
**图像腐蚀**
腐蚀操作是对所选区域进行“收缩”的一种操作,可以用于消除边缘和杂点。腐蚀区域的大小与结构元素的大小和形状相关。其原理是使用一个自定义的结构元素,如矩形、圆形等,在二值图像上进行类似于“滤波”的滑动操作,然后将二值图像对应的像素点与结构元素的像素进行对比,得到的交集即为腐蚀后的图像像素。
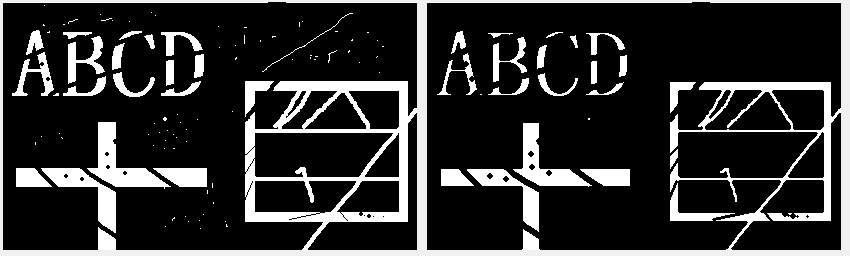
原图(左)、腐蚀后图像(右)
python实现:
```python
# 腐蚀
def erode(src, iterations=1):
h, w = src.shape[:2]
dst = copy.deepcopy(src)
tmp = copy.deepcopy(src)
for k in range(iterations):
for i in range(1, h - 1):
for j in range(1, w - 1):
if tmp[i][j] == 255: # 对图像点操作
mask = MORPH_CROSS
block = dst[i-1:i+2, j-1:j+2]
val = (block * mask).sum()
if val < 255 * mask.sum():
tmp[i][j] = 0
dst = copy.deepcopy(tmp)
return dst
```
**图像膨胀**
与腐蚀相反,膨胀是对选区进行“扩大”的一种操作。其原理是使用一个自定义的结构元素,在待处理的二值图像上进行类似于“滤波”的滑动操作,然后将二值图像对应的像素点与结构元素的像素进行对比,得到的并集为膨胀后的图像像素。
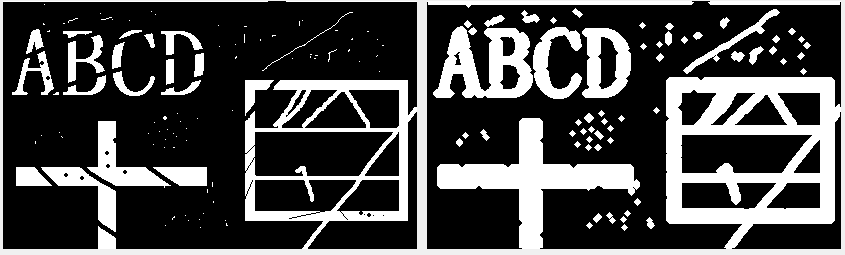
原图(左)、膨胀后图像(右)
python实现:
```python
# 膨胀
def dilate(src, iterations=1):
h, w = src.shape[:2]
dst = copy.deepcopy(src)
tmp = copy.deepcopy(src)
for k in range(iterations):
for i in range(1, h - 1):
for j in range(1, w - 1):
if tmp[i][j] == 0: # 对背景点操作
mask = MORPH_CROSS
block = dst[i-1:i+2, j-1:j+2]
val = (block * mask).sum()
if val >= 255:
tmp[i][j] = 255
dst = copy.deepcopy(tmp)
return dst
```
##### 8.连通域分析
在数字图像处理中,以位于坐标 (*x*, *y*) 处的像素点a为中心的相邻像素点称为点a的邻域,最为常见的是4邻域分析法和8邻域分析法。在视觉上看来,彼此连通的点形成了一个区域,而不连通的点形成了不同的区域。这样的一个所有的点彼此连通点构成的集合,我们称为一个连通区域。
连通区域(Connected Component)一般是指图像中具有相同像素值且位置相邻的前景像素点组成的图像区域(Region,Blob)。连通区域分析(Connected Component Analysis,Connected Component Labeling)是指将图像中的各个连通区域找出并标记。
python实现如下:
```python
# 连通域分析
def conc(src):
flag = 0
h, w = src.shape[:2]
labels = np.zeros((h, w))
# 粗检测 顺序检测 检测对象是src
for i in range(1, h-1):
for j in range(1, w-1):
if src[i][j] == 255: # 只对src中的图形点进行检测
block = labels[i-1:i+2, j-1:j+2] # 一个像素的8邻域
neighbors = [] # 连通域
for m in range(3):
for n in range(3):
if block[m][n] > 0: # 只取邻域中的标记
neighbors.append(block[m][n])
if not neighbors: # 列表为空,说明周围都没有标记,则开始一个新的连通域标记
flag += 1
labels[i][j] = flag
else:
labels[i][j] = min(neighbors)
# 复查 逆序检测 检测对象是labels
for i in range(h-2, 0, -1):
for j in range(w-2, 0, -1):
if labels[i][j] > 0: # 只对labels中标记的连通域进行检测
block = labels[i-1:i+2, j-1:j+2]
neighbors = []
for m in range(3):
for n in range(3):
if block[m][n] > 0:
neighbors.append(block[m][n])
labels[i][j] = min(neighbors)
# 重新映射灰度级
step = 255 // flag # 此时的flag已经是labels中的最大值
labels = labels * step
labels = labels.astype(np.uint8)
return labels
```
实验结果:
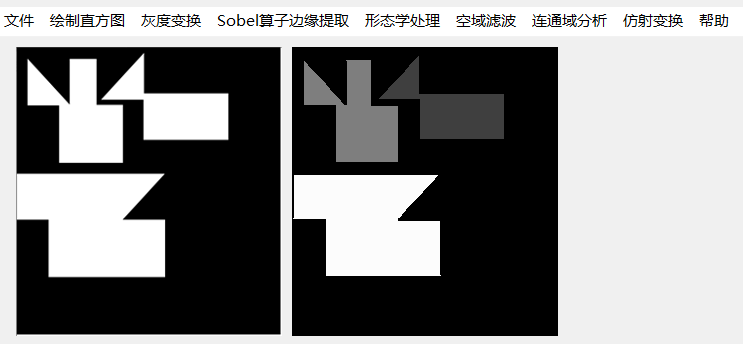
##### 9.其他
列表切片是python的一个很好用的特性,numpy数组也支持切片
```python
# 一维数组
a = np.array([1, 2, 3, 4, 5, 6, 7, 8])
b = a[:3] # b = [1, 2, 3] 表示从头开始到索引3之前的片
c = a[3:] # c = [4, 5, 6, 7, 8] 表示从索引3开始,一直到末尾
# 二维数组
a_2d = np.array([[1, 2, 3, 4],
[5, 6, 7, 8]])
b_2d = a_2d[0:2, 1:3]
# b = [[2, 3],[6, 7]]
# 多维数组
# 假设a_nd是彩色图像读取到numpy数组
a_nd[:, :, 0] # 表示r通道的所有像素值
```
numpy数组的广播机制:numpy数组在乘以一个数时,结果为数组所有元素乘以这个数(其他运算类似);numpy数组乘以一个相同形状的数组,结果为相同位置的数想乘 